A bi-modal distribution is a statistical distribution that has two peaks in its frequency distribution curve, indicating that there are two distinct groups or subpopulations within the data set. These peaks can be roughly equal in size, or one peak may be larger than the other. In either case, the bi-modal distribution is a useful tool for identifying and analyzing patterns in data.
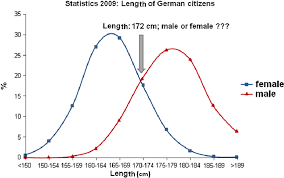
One example of a bi-modal distribution can be found in the distribution of heights among adult humans. The first peak in the distribution corresponds to the average height of adult women, which is around 5 feet 4 inches (162.6 cm). The second peak corresponds to the average height of adult men, which is around 5 feet 10 inches (177.8 cm). The two peaks in this distribution are clearly distinct, indicating that there are two distinct groups of people with different average heights.
To illustrate this bi-modal distribution, we can plot a frequency distribution histogram of heights of adult humans. The histogram would have two distinct peaks, one corresponding to the heights of women and the other corresponding to the heights of men. The histogram would also show that there is very little overlap between these two groups, indicating that they are largely distinct.
One of the main reasons why bi-modal distributions are important is that they can provide insights into the underlying structure of a data set. For example, in the case of the distribution of heights among adult humans, the bi-modal distribution indicates that there are two distinct groups with different average heights. This could be useful for a range of applications, from designing clothing to developing medical treatments.
Another example of a bi-modal distribution can be found in the distribution of income among households in the United States. The first peak in this distribution corresponds to households with low to moderate income, while the second peak corresponds to households with high income. This bi-modal distribution has been studied extensively by economists and policy makers, as it has important implications for issues such as income inequality and economic growth.
In conclusion, bi-modal distributions are a useful tool for identifying and analyzing patterns in data. They can provide insights into the underlying structure of a data set, and can be useful for a range of applications. The distribution of heights among adult humans and the distribution of income among households in the United States are two examples of bi-modal distributions that have important implications for a range of fields. A better understanding of bi-modal distributions can help us make better decisions and develop more effective solutions to complex problems.
